
DOMANDA: Nell'esercizio:
Due lamine Polaroid sono poste in contatto fra loro con un angolo di 0.020 radianti fra le loro direzioni di trasmissione. Un fascio di luce polarizzata linearmente con il piano di polarizzazione che forma un angolo di 0.337 radianti con la direzione di trasmissione del primo polaroid passa attraverso il sistema. Se l'ampiezza del fascio incidente è 319.8 volt/metro, qual è l'ampiezza del fascio emergente?
RISPOSTA:
La luce è un'onda elettromagnetica generata dalla vibrazione di cariche elettriche. Si tratta di un'onda trasversale, cioè il campo elettrico (e quello magnetico) oscilla perpendicolarmente alla direzione di propagazione dell'onda. Tuttavia queste oscillazioni in genere non avvengono in un piano fissato ma casualmente in tutte le direzioni. Quando un'onda ha questo comportamento si dice che è non polarizzata. La luce solare o quella di una lampadina è luce non polarizzata. Viceversa, un'onda il cui campo elettrico vibri in un piano fisso si dice polarizzata linearmente.

La luce non polarizzata può essere trasformata in luce polarizzata con molti metodi. Uno di questi è l'uso di lamine Polaroid. Queste lamine sono composte di materiale in cui l'allineamento delle molecole crea una direzione privilegiata, detta asse di trasmissione del Polaroid. La lamina lascia passare soltanto la componente dell'onda che vibra parallelamente all'asse di trasmissione, assorbendo tutte le componenti ad esso perpendicolari.

Se la luce che incide sul polarizzatore è non polarizzata, la luce che emerge è polarizzata linearmente nella direzione dell'asse di trasmissione del polarizzatore, e di intensità pari alla metà dell'intensità del fascio incidente. Se il fascio incidente è polarizzato, bisogna tener conto dell'angolo α tra la direzione di oscillazione del campo incidente e la direzione dell'asse di trasmissione del polarizzatore: la luce che emerge sarà soltanto la componente parallela all'asse di trasmissione, perciò l'ampiezza è uguale all'ampiezza iniziale moltiplicata per il coseno di α.
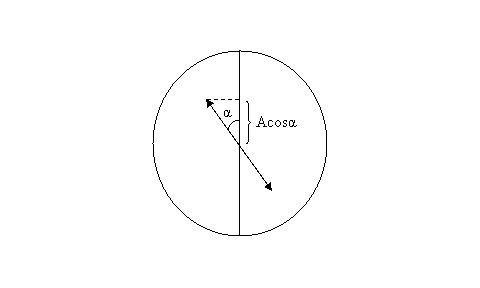
Se i polarizzatori sono più di uno basta iterare questo ragionamento. Per due polarizzatori con assi di trasmissione formanti tra loro un angolo β si avrà
A2 =cos(α).cos(β) A0
L'intensità di un'onda è proporzionale all'ampiezza al quadrato, perciò per un solo polarizzatore si avrà
I2 =cos2(α) I0
e per due
I2 =cos2(α).cos2(β) I0
NOTA: La dipendenza dell'intensità di un'onda dal quadrato della sua ampiezza è una relazione che vale per tutte le onde, longitudinali o trasversali, polarizzate o non polarizzate. Per ricavare questa relazione il modo più semplice è considerare un'onda sferica e calcolare l'energia che attraversa una superficie sferica mentre l'onda si propaga.
Link utili: Physics 2000: La polarizzazione
Per ulteriori informazioni, chiarimenti o suggerimenti manda un mail a:
Prof. F. L. Navarria (francesco.navarria .at. unibo.it)
Prof. T. Rovelli (tiziano.rovelli .at. cern.ch)
Prof. N. Moggi (moggi .at. bo.infn.it)
Dr.ssa N. Tinti (tinti .at. bo.infn.it)

Copyright © 2013 DFUB
Ultimo aggiornamento 2 Marzo 2013