NOTE
 Dopo un certo periodo di tempo
possiamo affermare che si e` formato all'interno del capillare uno stato
stazionario con un flusso della sostanza diffondente talmente piccolo da
non essere praticamente in grado di alterare nel tempo la concentrazione di
questa sostanza. Ponendo quindi
Dopo un certo periodo di tempo
possiamo affermare che si e` formato all'interno del capillare uno stato
stazionario con un flusso della sostanza diffondente talmente piccolo da
non essere praticamente in grado di alterare nel tempo la concentrazione di
questa sostanza. Ponendo quindi
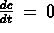 la seconda
legge di Fick diviene:
la seconda
legge di Fick diviene:

equazione differenziale facilmente integrabile con le condizioni
al contorno:
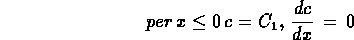
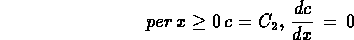
condizioni che stanno ad indicare come nelle espansioni la concentrazione
sia costante e l'agitazione perfetta, cosi` da non lasciare
alcun gradiente di concentrazione. Pertanto:
 (*)
(*)
 (*)
(*)
da cui, per x=0:

e, per x=1:

per cui le (*) diventano:
 (**)
(**)
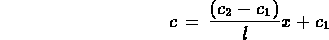 (**)
(**)
Quindi, quando si sono raggiunte le condizioni di stazionarieta`
il flusso della sostanza diffondente e` governato dal gradiente di
concentrazione costante (c2-c1)/l e la concentrazione
entro il capillare assume il profilo lineare descritto dalla seconda delle
(**).
 Ritorna alla misura del coefficiente di diffusione tramite
l'apparecchio di clack
Ritorna alla misura del coefficiente di diffusione tramite
l'apparecchio di clack
Copyright © I.S.H.T.A.R. - March, 1996
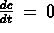 la seconda
legge di Fick diviene:
la seconda
legge di Fick diviene:

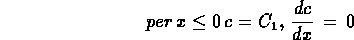
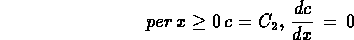
 (*)
(*)
 (*)
(*)


 (**)
(**)
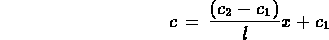 (**)
(**)