Come (e perchè) risolvere gli esercizi di Fisica

===============================

Una corretta tecnica nella soluzione di un esercizio, indipendentemente dalla sua difficoltà, è utile non solo per arrivare al risultato nel tempo più breve, ma anche per comunicarlo ad altri, incluso ad es. il docente, nel modo migliore.

Suggerimenti per la soluzione:

  • Disegnate uno o più diagrammi che schematizzano la situazione descritta nel testo del problema, in modo da chiarire la vostra analisi. Spesso ne basta uno. Nei disegni indicate le grandezze fisiche con lettere, mai con numeri.
  • [Vicino al disegno] sintetizzate in una tabella i dati del problema, rispettando la precisione dei valori (il numero di cifre) e le unità di misura specificate. Controllate di aver riportato correttamente non solo le cifre ma gli ordini di grandezza (esponenti, con il relativo segno); questa verifica deve essere fatta ad ogni ulteriore passaggio.
  • [Ri]leggete il testo dell'esercizio attentamente per essere sicuri di aver capito bene che cosa si richiede e in quale forma. Non trascurate le singole parole, due enunciati che differiscano anche solo per un monosillabo ('e' al posto di 'o', o viceversa) danno luogo a risultati diversi.
  • Ricavate la formula risolutiva dell'esercizio nella forma esplicita x = f(y,z,t...) dove x è la grandezza richiesta e y,z,t... sono le altre grandezze che intervengono nella soluzione. Questo vi permetterà di identificare eventuali grandezze ridondanti nell'enunciato. Verificate la correttezza dimensionale della formula risolutiva.
  • Scegliete il sistema di unità di misura, per es. quello in cui deve essere data la soluzione, oppure quello più comodo per fare i conti. Trasformate i valori delle grandezze che devono essere trasformate, tenendo conto della precisione finale richiesta (tre cifre significative) e quindi arrotondando nei passaggi intermedi a non meno di quattro cifre. Non trasformate più dello stretto necessario. Evitate il più possibile i passaggi intermedi: in ciascun arrotondamento è insita una approssimazione, quindi un errore, mentre il portarsi dietro troppe cifre non aiuta, appesantisce il foglio e fa aumentare il rischio di trascriverne male una, magari fra le prime, o addirittura un esponente.
  • Calcolate il valore richiesto, arrotondando il risultato al numrero di cifre significative richieste, tipicamente tre per un numero reale. A volte il risultato è intero ed è importante che lo sia.
  • Separatamente, per non appesantire la scrittura, controllate le unità.
  • Calcolate senza la calcolatrice almeno l'ordine di grandezza del risultato che vi aspettate. Ciò permette di verificare di non aver aver fatto proprio errori di calcolatrice (un esponente sbagliato ad es.) o altri grossolani errori di trascrizione.
  • Controllate infine che il risultato non violi il buon senso. Ciò può dipendere dai dati (sono scelti a caso), oppure dalla soluzione, ad es. un segno sbagliato o un esponente, un rapporto invertito. Un oggetto che nel vuoto e nel solo campo della gravità cade verso l'alto, una velocità maggiore della costante c di Einstein, una grandezza negativa sotto radice quadrata etc. segnalano la presenza di un errore.

    • If you can't solve a problem, you can always look up the answer. But please, try first to solve it by yourself; then you'll learn more and you'll learn faster [Donald E. Knuth, The TEXbook (1983)]

    Esempi di risoluzione degli esercizi

  • Esercizio 1

    • Un bambino lancia dei sassi contro una parete quadrata di lato 5.44 m in cui sono stati praticati 223 fori quadrati aventi un lato di 9.71 cm. Se il bambino non mira e i sassi sono piccoli rispetto alle dimensioni dei fori, qual'è il numero più probabile di sassi che rimbalzerà sulla parete ogni 590 lanci?

    Soluzione.

    La probabilità è data dall'area favorevole al passaggio dei sassi, cioè l'area complessiva dei fori, divisa per l'area totale della parete sulla quale sono lanciati uniformemente e casualmente i sassi. L'uso del calcolo delle probabilità è giustificato dall'assumere una distribuzione casuale e uniforme dei lanci (oppure un grande numero di fori ed una distribuzione uniforme e casuale dei fori stessi). Si ha quindi

    q = 1 - p = 1- (n a)/A = 1 - (n l2)/L2,

    dove q indica la probabilità che i sassi rimbalzino (p = 1 - q è quella che passino dall'altra parte), a = l2 è l'area di ciascuno degli n fori e A = L2 quella della parete. Il numero più probabile j di sassi che rimbalzano si ottiene moltiplicando q per il numero m di lanci e ricordando che j è intero (i sassi sono come gli elettroni o le persone!).

    j = m q = = m [1 - (n l2)/L2] = 590*[1-223*(0.0971/5.44)2] = 548

    Prima di fare il conto si è trasformata la lunghezza l in m (1 cm = 0.01 m). Alternativamente si poteva trasformare L in cm.

  • Esercizio 2

    • Il coefficiente di diffusione dell'emoglobina in acqua è D = 6.32*10-7 cm2sec-1 a temperatura ambiente (20 gradi C). Calcolare quanta emoglobina diffonderà lungo un tubo orizzontale con sezione di raggio 1.98 cm in 8704.4 ore sotto un gradiente di concentrazione di 4.472 g/litro per metro.

    Soluzione.

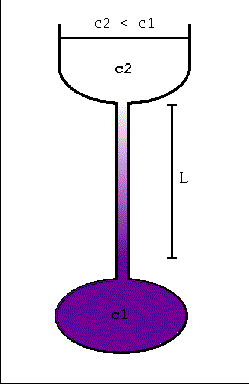
    Secondo i dati del problema abbiamo a che fare con la diffusione di un soluto in una soluzione in condizioni stazionarie [gradiente di concentrazione costante per cui vale la [prima] legge di Fick

    m = - D pi r2 dc/dx t .

    m è la massa di soluto che passa attraverso il tubo nel tempo t, D è il coefficiente di diffusione, A = pi r2 l'area di una sezione del tubo cilindrico, dc/dx [in figura è indicato come (c1-c2)/L] il gradiente di concentrazione. In figura il tubo è disegnato verticale, mentre nel testo si parla di un tubo orizzontale: nei limiti in cui si trascura l'effetto della gravità, questa differenza è irrilevante.
    L'unica difficoltà consiste quindi nella conversione delle unità di misura. Supponiamo di calcolare la massa di soluto diffusa in kg.

    D = 6.32*10-7 cm2sec-1 = 6.32*10-11 m2sec-1 -- ( 1 cm2 = 10-4 m2 )

    r = 1.98 cm = 1.98*10-2 m -- ( 1 cm = 10-2 m )

    dc/dx = 4.472 g/litro per metro = 4.472 kg/m4 -- ( 1 g/l = 1 kg/m3 )

    t = 8704.4 h = 3.1336*107 s -- ( 1 h = 3,600 s).

    Il risultato può essere ottenuto in un'unica sequenza di operazioni con la calcolatrice [senza passaggi intermedi e quindi minimizzando il rischio di errori di trascrizione]:

    m = 6.32*10-11 m2sec-1 3.14159.... (1.98*10-2)2 4.472 kg/m4 3.1336*107 s = 1.09*10-5 kg

    Numericamente si può notare quanto segue. Le conversioni che implicano potenze di 10 non hanno alcun effetto ai fini del numero di cifre significative con cui si ottiene il risultato, quindi basta usare lo stesso numero di cifre dei dati nel testo. Quando la conversione [ad es. da h a s] implica fattori che non sono potenze di 10, occorre fare attenzione a non perdere in precisione, senza però portarsi dietro cifre inutili: una regola è che occorre utilizzare nei passaggi intermedi almeno una cifra in più rispetto al numero di cifre con cui si vuole il risultato finale, in questo caso quindi, se vogliamo il risultato con tre cifre significative, i numeri nell'espressione devono averne almeno quattro - siccome il tempo dato nel problema aveva cinque cifre, queste sono state tenute nel passaggio intermedio - usare 3.134 invece di 3.1336 produce lo stesso risultato finale. Infine pi, cioè o pi-greco, è stato indicato con sei cifre, ma qualsiasi calcolatrice lo da tipicamente con 10 cifre per cui non ci si deve stare a preoccupare!

  • Esercizio 3

    • Due lamine Polaroid sono poste in contatto fra loro con un angolo di 0.3954 radianti fra le loro direzioni di trasmissione. Se un fascio di luce non polarizzata di ampiezza 137.5 volt/metro passa attraverso il sistema, qual'è l'ampiezza del fascio emergente?

    Soluzione. La luce è un'onda elettromagnetica trasversale, quindi polazzabile. In generale quando un fascio di luce polarizzata linearmente con la direzione di polarizzazione che forma un angolo 1 con l'asse di trasmissione di un polaroid si ha la legge di Malus

    A1 = A0 * cos(theta1),


    dove A0 e A1 sono le ampiezze (coincidono con i campi elettrici dell'onda e si misurano quindi ad es. in V/m) del fascio di luce, rispettivamente prima e dopo il polaroid. Se si hanno due polaroids uno dietro l'altro, con gli assi di trassmissione che formano un angolo theta2, il secondo vedrà il fascio di luce lasciato passare dal primo e basterà applicare ancora la legge di Malus

    A2 = A1 * cos(theta2) = A0 * cos(theta1) * cos(theta2).


    Nel caso in cui la luce incidente è non polarizzata, il vettore campo elettrico sarà orientato casualmente sul piano del polaroid e l'angolo mediamente formato con il suo asse di trasmissione sarà theta1 = 45 gradi, ossia cos(theta1) = 0.7071 . Si noti che non è affatto necessario convertire theta2 in gradi prima di calcolare il coseno, effettuando una operazione in più, basta impostare "RAD" su una normale calcolatrice scientifica. Risultato

    A2 = 137.5*cos(0.3954rad)*cos(45deg) = 8.97E+01 V/m

    Per ulteriori informazioni, chiarimenti o suggerimenti manda un mail a:
    Prof. F. L. Navarria (navarria@bo.infn.it)

    Copyright  ©  2000 DFUB