LE IPOTESI DI LAVORO

Per formulare leggi che regolino il moto dei fluidi consideriamo
un fluido ideale,
cioè un fluido incomprimibile e non viscoso; consideriamo
inoltre il caso che si muova di moto stazionario e
irrotazionale.
Nel moto stazionario la velocità
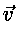 in ogni punto è costante nel tempo, cioè ogni particella che
transita per un qualsiasi punto P lo fa sempre con la stessa velocità in
modulo e verso. Perciò se tracciamo il percorso di una particella,
questo sarà anche il percorso di ogni altra particella che arriva in
P : lo spazio occupato dalla corrente è quindi proprio un
campo vettoriale.
in ogni punto è costante nel tempo, cioè ogni particella che
transita per un qualsiasi punto P lo fa sempre con la stessa velocità in
modulo e verso. Perciò se tracciamo il percorso di una particella,
questo sarà anche il percorso di ogni altra particella che arriva in
P : lo spazio occupato dalla corrente è quindi proprio un
campo vettoriale.
La curva che descrive il moto della particella si chiama linea
di flusso ed è tangente alla velocità della particella
in ogni suo punto.
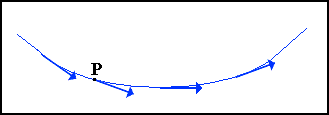
Nel moto stazionario le linee di flusso non si incrociano mai, in quanto
se lo facessero una particella che arriva al punto di incrocio potrebbe
proseguire lungo una linea o l'altra, quindi in uno stesso punto
potrebbe avere differenti valori di velocità, contrariamente
all'ipotesi stessa di stazionarietà.
È possibile quindi dire che per il moto stazionario esiste una sola
linea di flusso per ogni punto del fluido e che l'insieme delle linee di
flusso è fisso nel tempo. Prendendo un fascio di linee di flusso
otteniamo una superficie tubolare detta tubo di flusso
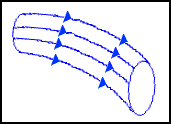
Per semplicità d'ora in avanti faremo coincidere il tubo di flusso con
il condotto reale entro il quale scorre il fluido, ma teniamo presente
la natura vettoriale del fluido un moto.
Per l'ipotesi di incomprimibilità del fluido osserviamo
che il volume del fluido che in un certo tempo attraversa la
sezione del condotto non varia con la sezione, altrimenti si avrebbe
accumulo o rarefazione di fluido in alcune regioni nelle quali la densità
aumenterebbe o diminuirebbe in contraddizione con l'ipotesi di incomprimibilità.
 Fluidi ideali > Equazione di continuità
Fluidi ideali > Equazione di continuità
 Fluidi ideali
Fluidi ideali
 Indice
Indice
Copyright © I.S.H.T.A.R. - March, 1999
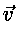 in ogni punto è costante nel tempo, cioè ogni particella che
transita per un qualsiasi punto P lo fa sempre con la stessa velocità in
modulo e verso. Perciò se tracciamo il percorso di una particella,
questo sarà anche il percorso di ogni altra particella che arriva in
P : lo spazio occupato dalla corrente è quindi proprio un
campo vettoriale.
in ogni punto è costante nel tempo, cioè ogni particella che
transita per un qualsiasi punto P lo fa sempre con la stessa velocità in
modulo e verso. Perciò se tracciamo il percorso di una particella,
questo sarà anche il percorso di ogni altra particella che arriva in
P : lo spazio occupato dalla corrente è quindi proprio un
campo vettoriale.
