

Per introdurre la distribuzione binomiale ricorriamo ad un
esempio.
Supponiamo che tre persone (Francesca, Luigi e Tiziano)
escono ciascuno dalla loro casa per andare a prendere il medesimo
autobus e che ciascuno di essi abbia probabilitÓ pari a p
di riuscire ad arrivare in tempo alla fermata (e ovviamente
probabilitÓ 1-p di perdere l'autobus): ci si chiede quale
sia la probabilitÓ che due dei tre personaggi in questione
riesca nell'intento.
Cominciamo col notare che si richiede la probabilitÓ che due prendano l'autobus, senza specificare quali: in questo modo l'evento due persone prendono l'autobus si pu˛ verificare in tre modi diversi ossia
Dunque l'evento almeno in due prendono l'autobus, che
denoteremo 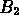 , sarÓ
rappresentabile come
, sarÓ
rappresentabile come
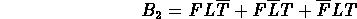
dove F, L e T sono rispettivamente
Francesca, Luigi e Tiziano che prendono l'autobus, mentre 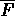 ,
, 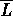 e
e 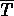 corrispondono ognuno al rispettivo
personaggio deluso per aver perso l'autobus.
corrispondono ognuno al rispettivo
personaggio deluso per aver perso l'autobus.
Potendo inoltre considerare i tre personaggi (eventi) indipendenti, per
i teoremi della somma e del
prodotto delle
probabilitÓ, la probabilitÓ dell'evento 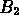 sarÓ:
sarÓ:
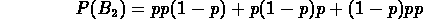
Ponendo 1 - p = q otteniamo in definitiva
P(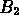 ) =
3 p2q
) =
3 p2q
Vediamo la generalizzazione di questo esempio.
Si considerino N prove indipendenti in cui l'evento A
pu˛ verificarsi o meno: sia p la probabilitÓ (costante
per ogni prova) che l'evento A si presenti e di
conseguenza 1-p=q la probabilitÓ che esso non si
verifichi. Cerchiamo la probabilitÓ 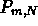 che l'evento A si verifichi m
volte in N prove.
che l'evento A si verifichi m
volte in N prove.
Consideriamo a questo proposito l'evento 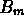 corrispondente al verificarsi di A
esattamente m volte in N prove.
corrispondente al verificarsi di A
esattamente m volte in N prove.
Come nell'esempio precedente questo evento pu˛ realizzarsi in
pi¨ modi diversi: decomponiamo allora l'evento 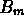 in una somma di prodotti
di eventi, consistenti nel presentarsi o meno di A in una
singola prova.
in una somma di prodotti
di eventi, consistenti nel presentarsi o meno di A in una
singola prova.
Se denotiamo con 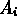 il
presentarsi dell'evento A nell'i-esima prova e con
il
presentarsi dell'evento A nell'i-esima prova e con 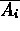 il non
presentarsi di A nell'i-esima prova, abbiamo che ogni
variante di apparizione dell'evento
il non
presentarsi di A nell'i-esima prova, abbiamo che ogni
variante di apparizione dell'evento 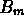 si compone di m apparizioni
dell'evento A e di n-m eventi
si compone di m apparizioni
dell'evento A e di n-m eventi 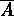 con indici distinti
con indici distinti
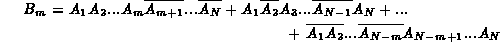
Il numero di combinazioni possibili Ŕ uguale a 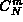 , cioŔ al numero di modi
diversi in cui si possono scegliere le m prove, tra le N
totali, in cui abbia luogo l'evento A.
, cioŔ al numero di modi
diversi in cui si possono scegliere le m prove, tra le N
totali, in cui abbia luogo l'evento A.
Per il teorema di
moltiplicazione delle probabilitÓ nel caso di eventi indipendenti, la
probabilitÓ di ogni combinazione Ŕ pmqN-m.
Essendo le varie combinazioni mutuamente escludentesi,
per il teorema dell'addizione,
la probabilitÓ dell'evento 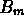 Ŕ pari a :
Ŕ pari a :
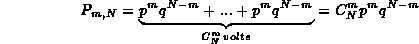
Il coefficiente 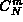 Ŕ detto coefficiente binomiale e viene spesso indicato
come
Ŕ detto coefficiente binomiale e viene spesso indicato
come 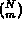 : in
particolare il suo valore Ŕ
: in
particolare il suo valore Ŕ
