

Soluzione. Prima di sparare i colpi sono possibili le seguenti ipotesi:
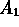 - Entrambi i tiratori mancano il bersaglio
- Entrambi i tiratori mancano il bersaglio 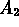 - Entrambi i tiratori centrano il bersaglio
- Entrambi i tiratori centrano il bersaglio 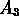 - Il primo tiratore centra il bersaglio, mentre
il secondo lo manca
- Il primo tiratore centra il bersaglio, mentre
il secondo lo manca 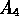 - Il primo tiratore manca il bersaglio, mentre il
secondo lo centra
- Il primo tiratore manca il bersaglio, mentre il
secondo lo centra Le probabilità di queste ipotesi valgono:
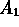 )
= 0.2
)
= 0.2 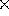 0.6 = 0.12
0.6 = 0.12 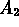 )
= 0.8
)
= 0.8 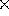 0.4 = 0.32
0.4 = 0.32 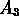 )
= 0.8
)
= 0.8 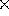 0.6 = 0.48
0.6 = 0.48 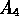 )
= 0.2
)
= 0.2 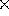 0.4 = 0.08
0.4 = 0.08 Le probabilità condizionate del verificarsi dell'evento X (bersaglio colpito una sola volta) per queste ipotesi sono uguali a:
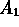 ) = 0
) = 0 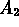 ) = 0
) = 0 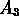 ) = 1
) = 1 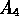 ) = 1
) = 1 Dopo la prova le ipotesi 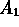 e
e 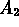 diventano impossibili, e le
probabilità delle ipotesi
diventano impossibili, e le
probabilità delle ipotesi 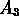 e
e 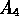 per la formula di Bayes sono:
per la formula di Bayes sono:
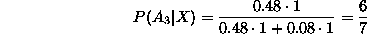
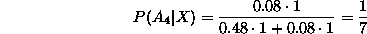
Di conseguenza la probabilità che il bersaglio sia stato colpito dal primo tiratore e pari a 6/7.
Soluzione. E` naturale supporre vera la comunicazione la cui probabilità di errore è minore: vediamo cosa accade applicando la formula di Bayes. A tale scopo impostiamo le ipotesi riguardanti lo stato dell'oggetto:
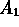 - L'oggetto si trova nello stato M
- L'oggetto si trova nello stato M 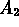 - L'oggetto si trova nello stato N
- L'oggetto si trova nello stato N In questo caso l'evento osservato X corrisponde al fatto seguente: la stazione n.1 ha trasmesso che l'oggetto si trova nello stato M e la stazione n.2 che esso si trova nello stato N. Le probabilità delle ipotesi prima dell'avvistamento sono:
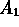 )
= 0.3
)
= 0.3 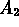 )
= 0.7
)
= 0.7 Calcoliamo le probabilità condizionate dell'evento
osservato X per queste ipotesi.
Affinchè l'evento X abbia luogo per l'ipotesi 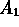 è necessario
che la comunicazione trasmessa dalla prima stazione sia
vera e quella proveniente dalla seconda sia errata,
cioè:
è necessario
che la comunicazione trasmessa dalla prima stazione sia
vera e quella proveniente dalla seconda sia errata,
cioè:
P(X | 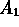 ) = 0.98
) = 0.98 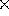 0.08 = 0.0784
0.08 = 0.0784
Analogamente
P(X | 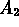 ) = 0.92
) = 0.92 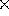 0.02 = 0.0184
0.02 = 0.0184
Applicando la formula di Bayes, troviamo la probabilità che lo stato reale dell'oggetto sia M:
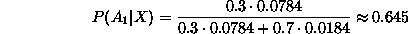
Cioè che la comunicazione della prima stazione fosse quella corretta.
 Il teorema delle ipotesi
Il teorema delle ipotesi