

Supponiamo che la grandezza che vogliamo calcolare sia z
= xy : nel calcolo dell'errore nei prodotti (o nei
quozienti) sfruttiamo gli errori relativi delle singole misure.
Utilizziamo però una forma leggermente diversa per esprimere i
valori delle quantità misurate direttamente in termini di errore
relativo, cioè:
valore misurato di x=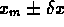 =
=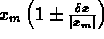
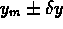 =
=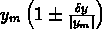 Ora, poichè
Ora, poichè 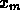 e
e 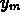 costituiscono le
nostre migliori stime per le grandezze x e y,
la stima migliore che possiamo fare della grandezza z
è proprio
costituiscono le
nostre migliori stime per le grandezze x e y,
la stima migliore che possiamo fare della grandezza z
è proprio 
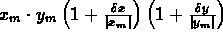 mentre il valore minimo
è dato da
mentre il valore minimo
è dato da
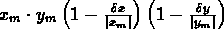 se ora andiamo a
sviluppare il prodotto delle due parentesi nel caso del
valore massimo (il discorso si può ripetere in modo
analogo per il valore minimo) otteniamo:
se ora andiamo a
sviluppare il prodotto delle due parentesi nel caso del
valore massimo (il discorso si può ripetere in modo
analogo per il valore minimo) otteniamo:
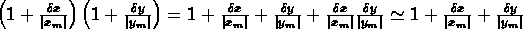 Si noti che
nell'ultimo passaggio si è usata l'uguaglianza
approssimata poichè abbiamo trascurato il prodotto dei
due errori relativi in quanto, essendo singolarmente
numeri piccoli (dell'ordine di qualche percento), il loro
prodotto è assai piccolo e trascurabile rispetto altre
quantità.
Si noti che
nell'ultimo passaggio si è usata l'uguaglianza
approssimata poichè abbiamo trascurato il prodotto dei
due errori relativi in quanto, essendo singolarmente
numeri piccoli (dell'ordine di qualche percento), il loro
prodotto è assai piccolo e trascurabile rispetto altre
quantità. Ne concludiamo in definitiva che le misure siffatte di x e y portano ad un valore di z=xy dato da:
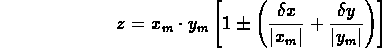
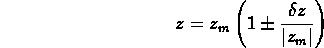
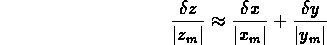
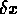 ,
, 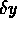 , ... ,
, ... , 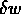 e tali valori vengono
utilizzati per calcolare quantità del tipo
e tali valori vengono
utilizzati per calcolare quantità del tipo allora
l'errore nel valore calcolato di z è pari alla
somma
allora
l'errore nel valore calcolato di z è pari alla
somma 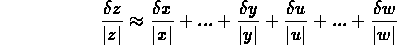
 Errori
nelle somme e differenze
Errori
nelle somme e differenze Errori
nell'elevamento a potenza
Errori
nell'elevamento a potenza