

La definizione della probabilità matematica è dovuta a A.N. Kolmogorov.
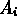 ) di un
esperimento
) di un
esperimento
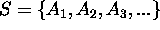 se
tali eventi sono mutuamente
escludentesi allora per ognuno di essi esiste una
probabilità P(A) rappresentata da un numero reale
soddisfacente gli assiomi di probabilità
se
tali eventi sono mutuamente
escludentesi allora per ognuno di essi esiste una
probabilità P(A) rappresentata da un numero reale
soddisfacente gli assiomi di probabilità
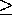 0 ;
0 ;
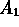 e
e 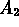 sono
eventi mutuamente escludentesi, allora deve
valere:
sono
eventi mutuamente escludentesi, allora deve
valere:
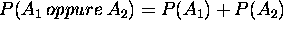
dove P (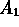 oppure
oppure 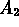 ) è la
probabilità di avere il risultato
) è la
probabilità di avere il risultato 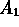 o il
risultato
o il
risultato 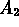
III) 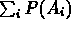 = 1 ,
dove la sommatoria è estesa su tutti gli eventi
mutuamente escludentesi.
= 1 ,
dove la sommatoria è estesa su tutti gli eventi
mutuamente escludentesi.
Le conseguenze dei tre assiomi sono:
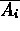 ) = P ( non
) = P ( non 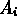 ) = 1 - P (
) = 1 - P (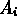 ), cioè
la probabilità di non ottenere l'evento
), cioè
la probabilità di non ottenere l'evento 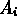 è uguale ad uno
meno la probabilità di ottenerlo.
è uguale ad uno
meno la probabilità di ottenerlo.
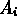 )
)  1,
cioè la probabilità è un numero reale appartenente
all'intervallo [0,1]: in pratica
1,
cioè la probabilità è un numero reale appartenente
all'intervallo [0,1]: in pratica 0  P (
P (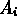 )
)  1
1
dove 1 rappresenta la certezza di ottenere l'evento 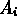 e 0 quella di non
ottenerlo.
e 0 quella di non
ottenerlo.