Le condizioni al contorno
Diffusione libera
Diffusione ristretta
Diffusione in stato stazionario
I metodi sperimentali per la misura del coefficiente di diffusione differiscono principalmente in base alle condizioni al contorno del fenomeno studiato
oltre che alle procedure analitiche seguite.
L'interpretazione dei risultati e` pero` semplificata nel caso in cui le condizioni al contorno sono tali da permettere di trovare una soluzione formale (analitica) dell'equazione differenziale di Fick.
i vari processi possono allora essere classificati come fenomeni di diffusione libera, diffusione ristretta e diffusione in condizione di stato stazionario. La specificazione del tipo di processo permette inoltre di scegliere la procedura sperimentale adatta alla misura del particolare coefficiente di diffusione coinvolto anche in ragione della precisione richiesta.
Avviene all'interfaccia soluto-solvente in una colonna verticale e puo` continuare finche non avviene un cambiamento di concentrazione al capo estremo della colonna di solvente. Nelle procedure di misura relative alla diffusione libera e` di primaria importanza disporre di interfaccie iniziali soluto-solvente quanto piu` nette possibile e di grandi rapporti tra le lunghezze della colonna di soluto e quella di solvente; a questo scopo sono state sviluppate varie tecniche chimico-fisiche.
Si attua dopo una diffusione libera, quando interviene il primo cambiamento di concentrazione all'estremo opposto della colonna di solvente. In caso di diffusione ristretta lineare, la presenza delle strutture di confinamento (pareti) che la caratterizza puo` dare origine anche a fenomeni diffusivi di tipo non lineare, per i quali non e` piu` valida lea legge di Fick (ad. es. fenomeni diffusivi in strutture fortemente capillari). Nel caso comunque di confinamenti sufficientemente "larghi", nei quali la legge di Fick continua spesso a valere e` necessario tenere presente la caratteristica fondamentale di questi tipi di diffusione: vale a dire, l'interdipendenza dei cambiamenti di concentrazione in tutti gli elementi di volume del sistema soluto-solvente.
In questo caso laconcentrazione e` mantenuta costante ai due capi con opportuni accorgimenti e, dopo un tempo sufficientemente lungo, si stabilisce un flusso stazionario costante e una distribuzione di concentrazione a gradiente costante. Condizioni al contorno di questo tipo offrono molti vantaggi nell'interpretazione dei risultati.
Infatti se il flusso J e il gradiente di concentrazione
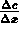sono misurabili sperimentalmente,
D puo` essere calcolato dalla prima
legge di Fick e non occorre integrare l'equazione
della seconda
legge, essendo stata eliminata ogni dipendenza temporale. Inoltre, dal
momento che i valori di c e di
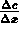possono essere misurati punto
per punto, D risulta completamente determinato.
Le difficolta` che comporta l'ottenimento di uno stato stazionario in una colonna ha scoraggiato molti sperimentatori. Il metodo rifrattometrico sviluppato da Clack ha pero` dato buoni risultati. In figura e` rappresentato uno schema dell'apparato usato da Clack.
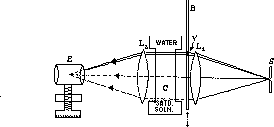
La colonna C in cui viene stabilito
lo stato stazionario ha le dimensioni
circa di 5 x 4 x 1 cm.
La parte finale della colonna termina in un recipiente contenente usa
soluzione satura in contatto con solido.
Un flusso costante e molto lento di acqua, tale da garantire l'assenza di
qualsiasi fenomeno vorticoso o turbolento, entra dall'estremita` superiore
della colonna; un analogo flusso in uscita dallo stesso livello assicura
che la concentrazione in questa zona sia essenzialmente nulla.
La misura di concentrazione
alle diverse altezze si ricava dalla misura
della variazione dell'indice di rifrazione che , a sua volta,
si ricava dallo
spostamento di un fascetto di luce
che attraversa la soluzione in modo perpendicolare.
Il flusso invece si calcola in base all'analisi della soluzione diluita che
giunge in cima
Misura del coefficiente di diffusione in caso di diffusione stazionaria
Ritorna alla analisi dal punto di vista macroscopico
Note
Indice
Approssimazioni