LA CAPILLARITÀ
Tubi di sezione molto piccola (del diametro
di qualche decimo di millimetro) sono detti vasi capillari:per questi
non vale più il principio dei vasi comunicanti. Nei tubi capillari
l'innalzamento o la depressione del livello del liquido dipende
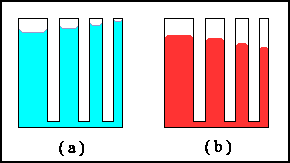
dal tipo di liquido (nel disegno sotto (a) è il caso dell'acqua che
tende a salire nei tubi e (b) quello del mercurio, che invece tende a
scendere) ed è inversamente proporzionale al raggio del tubo.
Se la superficie del liquido è concava verso l'alto la tensione
superficiale in corrispondenza delle pareti del tubo sarà diretta
verso il centro della superficie curva formata dal liquido e quindi
avrà una componente diretta verso l'alto. Il liquido, grazie a
questa forza, salirà nel tubo finché la forza verso l'alto dovuta
appunto alla tensione superficiale non sarà equilibrata dal peso del
liquido. È questa forza, quindi, che fa salire il liquido nei tubi
a sezione molto piccola o in materiali porosi.
Il fenomeno è spiegato dal fatto che
in un liquido esistono forze di coesione che fanno sì
che molecole simili si attraggano tra loro.
La forza tra la molecola di un liquido e un'altra sostanza (come il vetro
della parete di un recipiente che contenga il liquido stesso) è detta
forza di adesione.
Si dice che il liquido bagna la superficie di un'altra sostanza
quando le forze di adesione sono grandi rispetto le forze di coesione:
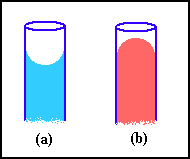
in questo caso la superficie di una colonna di liquido in un tubo (ad
esempio acqua in vetro) presenta una concavità verso l'alto (a) e si ha
la risalita del fluido in questione lungo un tubo capillare.
Se le forze di adesione sono piccole rispetto quelle di coesione (mercurio
in vetro) la superficie del liquido in un tubo è convessa (b) ed il livello
del fluido in un sistema di vasi capillari comunicanti tende a decrescere
al diminuire della sezione dei vasi.
Questo fenomeno è chiamato capillarità.
Applicazioni
Approfondimento matematico : ascensione capillare
Dinamica dei fluidi
La tensione superficiale
Indice
Copyright © I.S.H.T.A.R. - March, 1999