IL TEOREMA DI TORRICELLI

Da un foro posto ad una altezza (h) dalla superficie superiore di un
fluido contenuto in un serbatoio , il fluido esce con una
velocità pari a quella che avrebbe se scendesse in caduta libera per
un tratto (h).
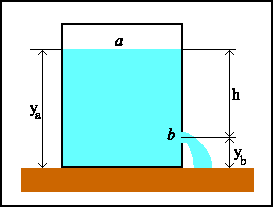
Ciò si dimostra applicando l'equazione di
Bernoulli ai punti (a) e (b) della figura. Supponendo che il diametro
del foro sia molto minore di quello del serbatoio, è possibile
trascurare la velocità dell'acqua in superficie, ovvero nel punto (a).
L'equazione di Bernoulli diventa:
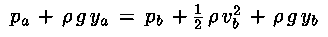
Essendo sia (a) che (b) in comunicazione con l'atmosfera, pa
e pb saranno uguali e pari alla pressione
atmosferica, quindi risolvendo rispetto vb:
![v(b)*v(b)=2g*[y(a)-y(b)]=2*g*h](/mflu/imgs/formule/torr2.gif)
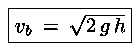
che è appunto la velocità che assumerebbe il fluido se cadesse
da (a) a (b) nel campo gravitazionale.
 Quesito
Quesito
 Esercizi
Esercizi
 Applicazioni
Applicazioni
 Storia
Storia
 Fluidi ideali > Effetto Magnus
Fluidi ideali > Effetto Magnus
 Fluidi ideali < Paradosso idrodinamico
Fluidi ideali < Paradosso idrodinamico
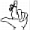 Indice
Indice
Copyright © I.S.H.T.A.R. - March, 1999

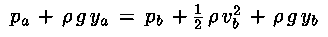
![v(b)*v(b)=2g*[y(a)-y(b)]=2*g*h](/mflu/imgs/formule/torr2.gif)
 Quesito
Quesito
 Esercizi
Esercizi
 Applicazioni
Applicazioni
 Storia
Storia