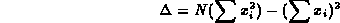Prima di passare al calcolo vero e proprio delle incertezze
sulle stime di A e di B vediamo di chiarire alcuni
punti sull'incertezza 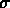 y.
y.
Bisogna ricordare che le y1...yN
non sono N misure della stessa grandezza: in questo
modo non possiamo farci un'idea della loro affidabilità solo
esaminando lo sparpagliamento dei loro valori.
Possiamo però stimare l'incertezza 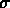 y nel modo seguente.
y nel modo seguente.
Partendo dall'assunto che ogni misura yi sia
normalmente distribuita attorno al suo valore vero Axi+B,
anche le singole deviazioni yi-Axi-B
sono normalmente distribuite, con lo stesso valore medio 0 e la
stessa larghezza 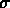 i.
Questo suggerisce che una buona stima per
i.
Questo suggerisce che una buona stima per 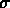 i dovrebbe essere
data dalla somma del quadrato degli scarti nella forma
i dovrebbe essere
data dalla somma del quadrato degli scarti nella forma
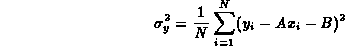
Tale stima, però, necessita di essere ulteriormente
raffinata: questo è dovuto al fatto che non conosciamo i valori
veri delle costanti A e B bensì li rimpiazziamo
con le nostre migliori stime. Questo rimpiazzo riduce leggermente
il valore precedentemente definito di 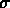 i: si può dimostrare
che è possibile compensare tale riduzione sostituendo il fattore
N del denominatore con il nuovo fattore N-2,
ottenendo così il risultato finale per
i: si può dimostrare
che è possibile compensare tale riduzione sostituendo il fattore
N del denominatore con il nuovo fattore N-2,
ottenendo così il risultato finale per 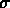 i
i
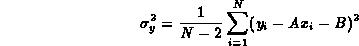
A questo punto possiamo passare al calcolo vero e proprio
delle incertezze sulle costanti A e B.
Essendo le stime di A e di B funzioni ben definite
dei valori misurati y1...yN, le
incertezze su tali stime si calcolano semplicemente applicando la
propagazione degli errori in termini di quelli in y1...yN,
percui si ottiene

e

dove al solito si è introdotta l'abbreviazione