

Occupiamoci ora del metodo analitico per ricavare la miglior
linea retta che interpola una serie di punti sperimentali, metodo
chiamato regressione lineare.
Per semplificare la trattazione, assumeremo d'ora in poi che le
incertezze si abbiano solo sulle grandezza in ordinata e che
tutte le incertezze siano uguali. Altro assunto (peraltro
ragionevole) che faremo č che ogni misura in y sia
governata dall distribuzione di Gauss, con lo stesso parametro 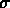 y per tutte le
misure.
y per tutte le
misure.
Quello che in pratica vogliamo determinare sono le due costanti A e B che determinano la retta migliore avente la forma
y = Ax + B
Se conoscessimo le costanti A e B allora per
ogni singolo  potremmo
calcolare il corrispondente valore vero di yi
come
potremmo
calcolare il corrispondente valore vero di yi
come
yi = Axi + B
poichč la misura yi č governata da una
distribuzione normale centrata su questo valore vero con
parametro 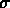 y, la
probabilitą di ottenere il valore osservato yi
č
y, la
probabilitą di ottenere il valore osservato yi
č
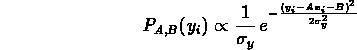
dove i pedici A e B indicano che questa probabilitą dipende dai loro valori che sono incogniti. La probabilitą di ottenere il nostro insieme completo di valori osservati y1...yN č
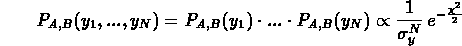
dove l'esponente č dato da
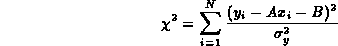
Le migliori stime per le costanti si ottengono imponendo che la probabilitą sia massima, in quanto gli yi cono i valori effettivamente osservati: questo equivale ad imporre che la somma dei quadrati nell'esponente sia minima. Per trovare tali valori differenziamo rispetto ad A e B e poniamo le derivate uguali a zero:
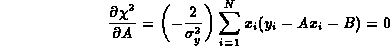
e
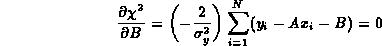
Queste due equazioni possono essere riscritte come:
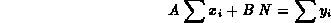
e
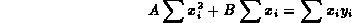
Tali equazioni, note anche come equazioni normali, una volta risolte, danno la stima delle costanti A e B
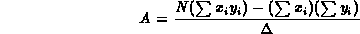
e
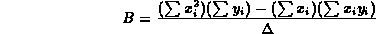
dove abbiamo introdotto l'abbreviazione
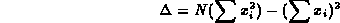
Calcolate le miglior stime delle costanti A e B dai valori misurati (xi,yi) č spontaneo chiedersi quali siano le incertezze nelle nostre stime.
 Incertezza
sulle costanti A e B
Incertezza
sulle costanti A e B