

Il caso di due variabili che soddisfano una relazione lineare del tipo y=Ax+B non è altro che un caso particolare di una vasta classe di problemi che riguardano le curve di adattamento, molti dei quali possono essere risolti in un modo similare. Vediamo ora alcuni di questi problemi.
Spesso accade che ci si aspetti che una variabile y sia esprimibile come una funzione polinomiale di una seconda variabile x, ossia
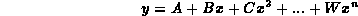
Dato un insieme di osservazioni delle due variabili, si può trovare la migliore stima delle A,B,...,H con un procedimento analogo a quello con cui abbiamo stimato le costanti A e B nel caso della relazione lineare. Per semplificare la trattazione supponiamo che la polinomiale sia di fatto una quadratica del tipo

Al solito supponiamo di avere una serie di misure con
incertezze solo sulla variabile dipendente (y) e che tali
incertezze siano tutte uguali. Allra per ogni  , il corrispondente valore vero di yi
è dato dalla funzione quadratica con A, B e C
incogniti. Assumendo che le misure degli yi
siano governate da distribuzioni normali, ciascuna centrata
sull'appropriato valore vero e tutte con lo stesso
, il corrispondente valore vero di yi
è dato dalla funzione quadratica con A, B e C
incogniti. Assumendo che le misure degli yi
siano governate da distribuzioni normali, ciascuna centrata
sull'appropriato valore vero e tutte con lo stesso 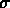 i, possiamo calcolare
la probabilità di ottenere proprio i valori osservati
y1...yN
come
i, possiamo calcolare
la probabilità di ottenere proprio i valori osservati
y1...yN
come
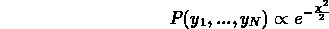
dove ora
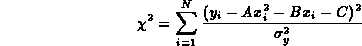
La miglior stima per A, B e C è data da
quei valori percui la probabilità è massima, ossia quando
l'esponente  2
è minimo.
2
è minimo.
Differenziando  2
rispetto a A, B e C e ponendo queste
derivate uguali a 0, otteniamo le tre "equazioni
normali"
2
rispetto a A, B e C e ponendo queste
derivate uguali a 0, otteniamo le tre "equazioni
normali"
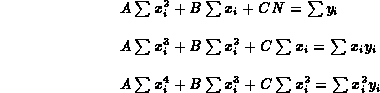
Per un dato insieme di misure queste equazioni simultanee per A, B e C possono essere risolte per trovare le miglior stime di A, B e C. Con A, B e C calcolati in questo modo l'equazione

è chiamata adattamento polinomiale dei minimi quadrati per le misure date. Sfortunatamente, soprattutto quando il grado delle polinomiali aumenta, non sempre le equazioni normali sono risolvibili oppure sono estremamente difficili, nonostante questo esiste una grande classe di problemi che possono essere risolti.
Data l'importanza della funzione esponenziale in fisica,
vediamo anche questo caso.
Consideriamo la funzione

Per ricondurci ad una forma a noi più familiare, applichiamo una "linearizzazione" della funzione applicando la funzione logaritmo: in questo modo otteniamo

Questa operazione, anche se non rende lineare y nei
confronti di x, fa sì che il logaritmo di y lo sia.
L'utilità di questa nuova relazione è facilmente verificabile.
Se riteniamo che x e y debbano soddisfare
l'equazione esponenziale, allora le variabili x e z=ln(y)
dovrebbero soddisfare

Se abbiamo una serie di misure (x,y), allora per ogni yi calcoliamo z=ln(y). Le coppie (zi,yi) dovrebbero giacere su una linea retta: tale retta può essere adattata con il metodo dei minimi quadrati, come abbiamo già visto, per ricavare le stime delle costanti A e B.
Dopo aver parlato di problemi a due variabili, vediamo un esempio con tre variabili (in molti problemi reali più di due variabili che vanno considerate: si pensi ad esempio alla relazione tra pressione volume e temperatura nei gas).
L'esempio più semplice (noi ci limiteremo a questo) è quello in cui una variabile dipende linearmente dalle altre due:

Se abbiamo una serie di misure (xi,yi,zi) con tutti gli zi ugualmente incerti e gli xi e yi privi di incertezza, possiamo procedere in modo analogo al caso dell'adattamento ad una retta: in questo caso la miglior stima per le costanti è data dalle equazioni normali
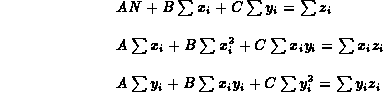
Questo metodo è chiamato regressione multipla