Per capire il criterio di Chauvenet per il rigetto dei dati consideriamo un esempio. Supponiamo di aver effettuato dieci misure di una certa grandezza X e di averle riassunte nella seguente tabella:
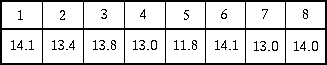
Se ora procediamo al calcolo della
media
(
) e della
deviazione standard
(
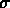) troviamo i valori:
= 13.4
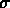= 0.8
In questa serie di misure il quinto valore (11.8) è
decisamente in disaccordo con tutti gli altri: vediamo come
procedere nei confronti di tale valore.
Dobbiamo prima di tutto quantificare quanto la misura in
questione sia anomala rispetto alle altre: per fare questo,
notiamo che il valore 11.8 si discosta dal valor medio di due
volte la deviazione standard.
Se assumiamo che le misure si conformino ad una distribuzione di
Gauss avente media e
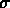deviazione standard allora
siamo in grado di calcolare la probabilità di avere misure che
differiscano dalla media di almeno due deviazioni standard.
La probabilità di avere tali misure si ottiene, secondo la proprietà
degli eventi contrari, sottraendo da uno (il 100%
rappresentante la globalità degli eventi) la probabilità di
ottenere risultati entro due deviazioni standard, cioè:
=
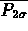1 -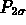 
dove con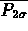
si intende appunto la probabilità di ottenere valori al di fuori
di 2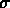 e con
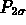la probabilità
di ottenerne entro 2.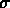
Da quanto detto, andando a vedere il valore tabulato di
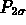, otteniamo:
=
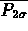1 - 0.95 = 0.05
In pratica abbiamo il 5% di probabilità di ottenere una
misura al di fuori di due deviazioni standard, cioè ci si deve
aspettare che una misura su venti si discosti di più di 1.6
unità (2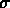) dal
valor medio (che nel nostro caso era 13.4).
Avendo noi eseguito otto misure, per la proprietà delle
probabilità di eventi indipendenti, il numero di misure oltre
2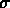 è dato da:
n = 0.05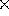 
8 = 0.4
Significa che mediamente ci si dovrebbe aspettare 2/5 di una
misura anomala come il nostro 11.8: in questo modo abbiamo
quantificato l'anomalia del valore in questione.
Ora si tratta di stabilire quale sia la "soglia di
accettabilità" per i dati dopodichè andiamo a vedere se il
dato incriminato deve essere rigettato o meno.
Di solito viene stabilita tale soglia ad 1/2, percui se il
numero atteso (n) di misure anomale è minore di 1/2, la misura
sospetta deve essere rigettata: da questo discende che il
nostro valore 11.8 non è da considerarsi ragionevole e quindi
deve essere rigettato.
Una volta capito questo esempio, la generalizzazione del
criterio ad un problema con più dati è immediata: si supponga
di avere N misure (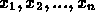
) della stessa granezza X.
Come prima cosa calcoliamo e 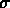dopodichè osserviamo i dati per
vedere se esiste qualche valore sospetto. Nel caso ci sia un dato
sospetto (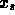
)
calcoliamo il numero di deviazioni standard
(
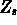) di cui
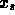differisce da
applicando la formula:
Fatta questa operazione bisogna andare a vedere quale è la
probabilità che una misura differisca da
di
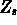volte la deviazione
standard: per fare questo bisogna ricorrere ai valori della
probabilità in funzione del numero di deviazioni standard
che si trovano facilmente tabulati.
Alla fine, per ottenere il numero (n) di misure anomale
che ci si aspetta, moltiplichiamo la suddetta probabilità per il
numero totale di misure (N):
n = N 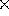P
(oltre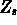
)
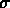Se il numero n è minore di 1/2 allora non si attiene al criterio di Chauvenet e come tale deve essere rigettato.
A questo punto si presenta uno spinoso problema:
come agire con i dati rimasti?
C'è chi sostiene che si debba applicare nuovamente il criterio
di Chauvenet ai dati rimasti (tenendo conto che dopo
l'eliminazione del primo dato si hanno diversi valori di e 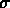) fintanto che tutti i dati
rimasti siano conformi al criterio di Chauvenet, mentre altri
sostengono che tale metodo non vada applicato una seconda volta
ricalcolando la media e la deviazione standard. Esiste però
anche un terzo modo, forse il più equilibrato anche rispetto a
coloro che ritengono che il rigetto di un dato non sia mai
giustificato, di affrontare il problema: molti scienziati infatti
utilizzano il criterio di Chauvenet non per scartare
immediatamente il dato, bensì solamente per individuarlo:
una volta individuato il valore sospetto si procede alla verifica
della sua attendibilità attraverso la riproduzione delle misure
e una successiva rianalisi dei dati.
Nota
La scelta dei dati
Il
criterio "a priori"