Il test del chi-quadrato riveste un ruolo fondamentale tra i
vari tipi di controlli statistici che si possono effettuare su
sequenze di numeri casuali: infatti tutti gli altri test che
abbiamo elencato (seriale, poker,...) si riconducono ad
un'analisi di grandezze secondo il test chi-quadrato.
Senza esporre nuovamente la parte relativa alla teoria
del test, andiamo a vedere come operativamente viene applicato su
sequenze di numeri random.
Supponiamo di avere a che fare con una sequenza di numeri
casuali distribuiti nell'intervallo [0,1): vogliamo
controllare se tali valori possono essere considerati alla
stregua delle realizzazioni di una variabile casuale U
uniformemente distribuita all'interno di tale intervallo.
La prima cosa da fare è dividere l'intervallo [0,1) in k
sottointervallli, ad esempio 100:
Dopodichè generiamo N numeri casuali ui,
per esempio 100000. Ci aspettiamo che questi 100000 numeri si
equipartiscano nei 100 sottointervalli. Naturalmente in ogni
intervallo non ne cadranno esattamente N/k, ma,
diciamo, ni.
Quanto vicino ad N/k deve essere ciascun valore ni
perchè la sequenza sia accettata?
Seguendo la filosofia tipica del test del 
2, si considera la
quantità
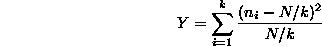
Nel caso in cui il numero di intervalli sia abbastanza grande
e lo sia anche ogni ni, la variabile Y
segue la distribuzione 2 con k-1 gradi
di libertà. Fissato un livello di confidenza a (di
solito: 0.01 o 0.05), tavole o codici numerici forniscono il
valore a2
tale che la probabilità che la variabile casuale 2 assuma
un valore maggiore di a2
sia uguale ad a.
Controlli
statistici