- Il criterio del
 2
-
2
-  2
-
2
- 
Il test del  2
(o, come talvolta viene chiamato, di Pearson) viene usato come
una sorta di "verifica delle ipotesi".
2
(o, come talvolta viene chiamato, di Pearson) viene usato come
una sorta di "verifica delle ipotesi".
Le ipotesi in questione possono riguardare semplicemente la
presenza o meno di una correlazione tra diverse variabili (in
questo caso si parla di verifica dell'indipendenza);
oppure riferirsi alla distribuzione teorico-matematica che meglio
riproduce i dati sperimentali (allora si parla di verifica
dell'aggiustamento).
In entrambe i casi il problema è quello di paragonare i
risultati sperimentali con le previsioni teoriche e di valutare
la distanza globale tra i due insiemi sommando i contributi di
ciascun elemento. Questi contributi sono valutati
percentualmente, cioè come rapporto tra lo scarto (differenza
tra risultato e previsione) e la previsione. Gli scarti sono
successiavamente elevati al quadrato per sopprimere il segno.
La distanza globale che che cerchiamo, detta appunto  2, è data
da:
2, è data
da:
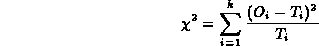
dove Oi sono i risultati osservati e Ti
le previsioni. Il  2
è tanto più grande quanto meno l'osservazione è compatibile
con le ipotesi. Siccome il
2
è tanto più grande quanto meno l'osservazione è compatibile
con le ipotesi. Siccome il  2 è calcolato utilizzando
dati sperimentali è esso stesso una variabile aleatoria che
segue, appunto, la distribuzione
2 è calcolato utilizzando
dati sperimentali è esso stesso una variabile aleatoria che
segue, appunto, la distribuzione
 2 nel
caso in cui i dati seguano la distribuzione normale.
2 nel
caso in cui i dati seguano la distribuzione normale.
Esistono tabelle e grafici che forniscono, in funzione del numero
di gradi di libertà dell'insieme, cioè del numero di contributi
che si sommano, i livelli di confidenza che corrispondono a
diversi valori di  2,
dicono cioè qual'è la probabilità di ottenere un
2,
dicono cioè qual'è la probabilità di ottenere un  2 maggiore o
uguale a quello osservato se l'ipotesi è vera.
2 maggiore o
uguale a quello osservato se l'ipotesi è vera.
L'uso del  2
come verifica dell'aggiustamento è concettualmente simile al
procedimento che abbiamo descritto. Si costruisce l'istogramma
dei dati e si ipotizza che essi seguano una certa distribuzione
teorica. Per verificare l'ipotesi si calcola il
2
come verifica dell'aggiustamento è concettualmente simile al
procedimento che abbiamo descritto. Si costruisce l'istogramma
dei dati e si ipotizza che essi seguano una certa distribuzione
teorica. Per verificare l'ipotesi si calcola il  2 secondo la
stessa definizione data sopra, utilizzando come Oi le
altezze delle colonne dell'istogamma e come Ti i
corrispondenti valori teorici. Anche in questo caso il
2 secondo la
stessa definizione data sopra, utilizzando come Oi le
altezze delle colonne dell'istogamma e come Ti i
corrispondenti valori teorici. Anche in questo caso il  2 ottenuto
è una variabile aleatoria e bisogna consultare le tabelle per
poterne derivare una conclusione quantitativa in termini di
probabilità. Per la verifica dell'aggiustamento il numero di
gradi di libertà è dato da
2 ottenuto
è una variabile aleatoria e bisogna consultare le tabelle per
poterne derivare una conclusione quantitativa in termini di
probabilità. Per la verifica dell'aggiustamento il numero di
gradi di libertà è dato da
n=k-np-1
dove k è il numero di colonne dell'istogramma
e np il numero di parametri della
distribuzione teorica (ad esempio 3 per la distribuzione di Gauss,
2 per la distribuzione di
Poisson, ...).
Se il  2
ottenuto è inferiore al valore che secondo le tabelle
corrisponde ad un livello di confidenza maggiore o uguale al 95%,
di solito l'ipotesi viene accettata: questo significa infatti
che, se i dati seguono effettivamente la distribuzione teorica
che stiamo verificando, la probabilità di avere per
fluttuazione statistica un
2
ottenuto è inferiore al valore che secondo le tabelle
corrisponde ad un livello di confidenza maggiore o uguale al 95%,
di solito l'ipotesi viene accettata: questo significa infatti
che, se i dati seguono effettivamente la distribuzione teorica
che stiamo verificando, la probabilità di avere per
fluttuazione statistica un  2 minore di quello
osservato è soltanto del 5%.
2 minore di quello
osservato è soltanto del 5%.
 Il
criterio "a priori"
Il
criterio "a priori"
 Rappresentazione grafica dei dati:
l'interpolazione
Rappresentazione grafica dei dati:
l'interpolazione
