Occupiamoci ora di come sia possibile stimare una quantità
incognita attraverso il metodo statistico di Monte Carlo.
Nel nostro caso si trattera della stima di un integrale.
Va detto che molto spesso altri metodi numerici di risoluzione
sono più consigliabili ed efficaci; ciò nondimeno, per
integrali multidimensionali il Monte Carlo può risultare
competitivo o, addirittura, la scelta più opportuna quando il
confine che delimita il dominio di integrazione è complicato,
l'integrando non esibisce picchi concentrati in regioni molto
ristrette e, infine, non si pretende un'accuratezza molto
elevata.
Cominciamo con un semplice integrale:
dove la f(x) è una funzione continua
sull'intervallo di integrazione [a,b].
Riscriviamo la precedente come:
dove p(x) è una qualsiasi funzione densità di
probabilità definita in [a,b].
Sia X una variabile casuale con densità di
probabilità p(x) e sia G la
variabile casuale definita da:
Poichè, per la definizione di valore atteso, si ha:
nel nostro caso ne consegue che
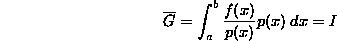
La valutazione di un integrale diventa, pertanto, un problema
risolvibile in chiave statistica, stimandone il valore mediante
l'esame di un opportuno campione.
Detta g una generica realizzazione della variabile
aleatoria G, la stima dell'integrale I
diventa:
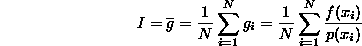
Siffatto metodo, in cui un integrale è rappresentato come un valore medio, è detto Monte Carlo grezzo
Il
metodo del "chiama e scarta"