Campo elettrico in un conduttore

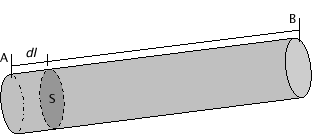
Consideriamo un conduttore cilindrico di sezione S e lunghezza l, di estremi A e B, percorso dalla corrente I.

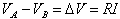
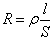
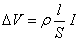
Supposto un conduttore omogeneo, si consideri il campo elettrico E uniforme; dunque se ∆V = E · l, allora:

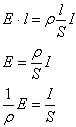
Si introduce la densità di corrente

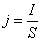
come la corrente che passa attraverso l'unità di area del conduttore, ovvero la carica che attraversa l'unità di superficie nell'unità di tempo, si ottiene:

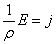
Segue la definizione di resistività

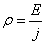
Talvolta si preferisce usare il reciproco della resistività, detto conduttività o conducibilità

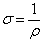
Conseguentemente

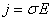
Questa relazione riassume le due leggi di Ohm e può essere assunta come definizione alternativa di conduttori ohmici.

Calcolo della velocità di deriva (drift velocity)

Detto n il numero delle cariche per unità di volume nel conduttore, la carica per unità di volume è (q n), con q = -e per gli elettroni.
La velocità delle cariche è

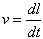
Il tratto di conduttore percorso nellÕintervallo di tempo dt è:

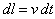
Attraverso la superficie S nel tempo dt passa una quantità di carica

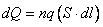
(S ·dl) rappresenta il volume del cilindro di base S ed altezza infinitesimale dl occupato dalle cariche che hanno attraversato S.

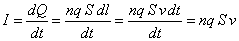
Dividendo primo e secondo membro per S, si otteniene:

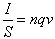
Quindi

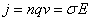
Segue che la velocità v delle cariche, detta velocità di deriva o drift, è costante perchè dipendente solo da grandezze costanti
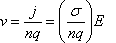